The Discrete Fourier Transform, But With Triangles

Here’s something I’ve been wondering about lately: what happens if you replace all the sine waves in the fourier transform with triangle waves? If you are like me and would like to play around with such a thing, this post has a method to get a representation of a signal as scaled-and-shifted band-limited triangle waves in $O(n\log n)$ time. This is fast enough that we can compute first and ask questions about what it’s good for later (I’ve yet to find anything). Actually, the stuff in this post will work for any periodic function, not just triangle waves, but this was the idea that motivated me to figure this out.

To get more precise in what I’m trying to do here, here’s what I want. The DFT takes a signal made up of sine waves with amplitudes $a_k$, phases $\theta_k$, and integer frequencies $k$, and produces a signal that has the value $a_ke^{i\theta_k}$ at $k$. I want a transform that does the same for triangle waves.

I had a few bad starts on this–for one thing, triangle waves are not orthogonal to each other at all–but it all came together when I asked the following question: What is a cosine wave given as a sum of triangle waves?

First, we need a definition of a triangle wave. With $K$ being the number of harmonics and $m = 2k + 1$,

$\text{tri}(x) = \sum_{k=0}^{K-1} \frac{1}{m^2} \cos(2\pi mx).$

I’ve adapted¹ this from the first of many definitions of a triangle wave on Wikipedia, where it’s presented without justification or citation. Personally, I don’t understand where it comes from, but it is pretty much the frequency domain represention of a triangle wave and that’s all we need. For the rest of this post, I’m going to leave $K$ implicitly defined as the largest value it can take without introducing aliasing in its current context.

For now, we just want to think about finding the $X_k$ that gives us

$\cos(2\pi \textbf{x}) = \sum_{k=0}^{N-1} X_k\text{tri}(k\textbf{x})$

where $\textbf{x}[n] = n/N$. Restricting ourselves to band-limited triangle waves gives us the fact that the lowest frequency of $\text{tri}(k\textbf{x})$ is $k$. Then $\text{tri}(\textbf{x})$ with $k = 1$ is the only member of our series that is not orthogonal to $\cos(2\pi \textbf{x})$, so we know $X_1 = 1$. But this introduces odd harmonics all the way up, and so the coefficient of the next odd triangle wave at $k = 3$ must use its lowest frequency to subtract out the first odd harmonic of the triangle wave at $k = 1$, so $X_3 = -1/9$. This adds yet more harmonics for later triangle waves to clean up. We keep going like this until we’ve accounted for all $N$ triangle waves.

If that was too quick, here it is in pictures. The frequency domain representation is overlaid on top.

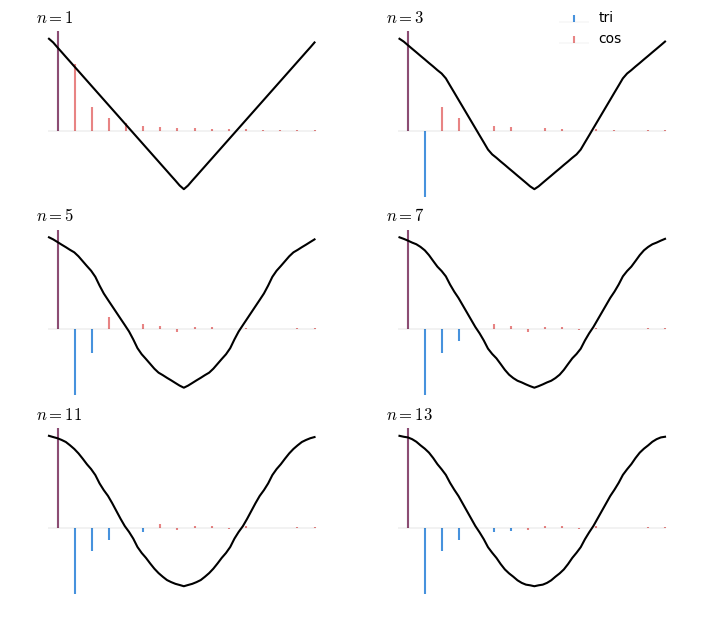
It’s not hard to see that this logic mostly works for arbitrary functions, too. We lose the orthogonality to kick off the process, but the whole point of the DFT is that sines and cosines form an orthogonal basis, so we only need orthogonality to the lowest frequency. As we go, we successively remove frequencies, so there is always a new lowest frequency to remove².

Before we can implement this we also need to handle the phase of each frequency component. When we see $a_ke^{i\theta_k}$ at $k$, we need to align the phase of the lowest frequency of $\text{tri}(kx)$ with $\theta_k$. We’re working in the frequency domain, so we need this thing from the shift theorem

$X_n e^{-i2\pi n\ell/N}$

to apply a shift of $\ell$. In our case, $X$ contains the $1/m^2$ factors of the current triangle wave. We just need to know $\ell$. Now, the lowest frequency of $\text{tri}(kx)$ is $X_k$, so we want to choose $\ell$ to satisfy

$X_n e^{-i2\pi n\ell/N} = X_k e^{i\theta_k} \quad \text{if } n = k.$

So

$\ell_k = -\frac{N}{2\pi}\frac{1}{k} \theta_k.$

This part seemed obvious when I was just turning ideas in my head into code but now that I write it out like this I’m not so sure.

This is all we need to find the $X_k$ in

$f(\textbf{x}) = \sum_{k=0}^{N-1} |X_k|\text{tri}(k\textbf{x} + \frac{1}{2\pi}\arg(X_k)).$

Iterative algorithms spelled out in maths notation always feel a bit clunky to me, so rather than doing that, here’s some Python code to do it:

import np

def cis(t):
    return np.cos(t) + 1j*np.sin(t)

def inverse_tri_sum_bandlimited(x):
    assert(np.isrealobj(x)) # real signals only. i'm lazy

    n = len(x)
    nyquist = n // 2

    y = np.fft.fft(x)

    m = np.arange(3, nyquist, 2)
    coefs = 1 / (m*m)

    for k in range(1, nyquist//2):
        # indices of the non-zero components of a triangle wave
        # with fundamental frequency k, not including the fundamental
        nz = np.arange(k*3, nyquist, k*2)
        # construct the frequency domain of the triangle wave and subtract it off
        y[nz] -= np.abs(y[k]) * coefs[:len(nz)] * cis(nz * (np.angle(y[k]) / k))

    # fix up conjugate symmetry
    y[nyquist+1:] = np.conj(y[nyquist-1:0:-1])

    return y

This makes use of the observation that once a frequency in y has been zeroed out we never look at it again, so we can do the algorithm in-place. Also, band-limited triangle waves above half the nyquist frequency are just sine waves, so we don’t need to consider them at all.

Some Graphs To Think About

The nice thing about this algorithm is the result is in the same representation as given by the DFT. So, if the DFT is $\mathcal{F}$ and our triangle transform is $\mathcal{T}$, then we can replace all the triangle waves in a function with sine waves by applying $\mathcal{F}^{-1}\mathcal{T}$. Right? So, this does what you might expect:

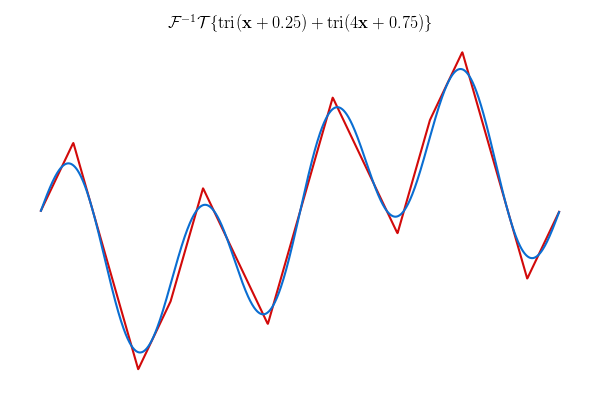
But look at this:

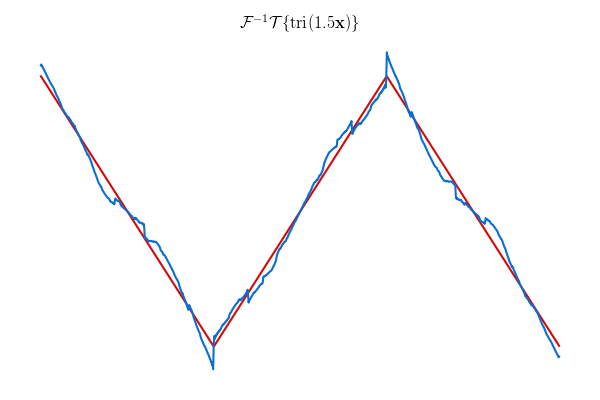
What gives? Well, this is a problem the DFT has, too. We’re getting a representation of the signal as a sum of triangle waves but $\text{tri}(1.5\textbf{x})$ isn’t one of them. In the analogous case for the DFT this isn’t so bad because it ends up being represented by nearby sine waves. You get a nice exponential drop-off away from the true frequency. For triangle waves, you don’t have that at all. Now, this is without windowing, so there is also a big jump between the last and first sample that we probably ought to do something about. Maybe if we apply a triangular window…

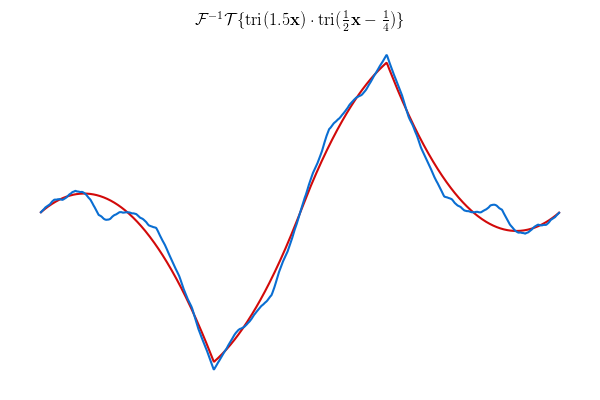
I don’t know what I expected.

Anyway, the reason I did all this was to see if anything interesting happened when you messed around with it. For example, we can swap out $\mathcal{F}$ for $\mathcal{T}$ in the convolution theorem. Here is a gaussian filter applied in the “triangle domain”, with $\sigma=2$ and with $\sigma=100$. Image from Wikimedia.

Interesting! I don’t really have an intuition for what’s happening on for $\sigma = 2$. Larger values of $\sigma$ look a bit more like what I expected.

I also tried filtering audio this way. Removing high frequency triangle waves–maybe I should give those a cute name like triquencies, because strictly speaking each one is multiple frequencies so I find it weird to refer to them that way–introduces high harmonics of low frequency content in the signal. This sounds really nice if you have something with lots of harmonic material–you get a nice wash of soft sawtooth buzz–and pretty bad on something with sparse hamonics, like a plucked string. It would be nice to be able to use this for some audio effect, buuut $\mathcal{T}$ isn’t linear, so you can’t use the usual methods to convolve small filters with long signals. Oh, well.

Odds and Ends

$O(n\log n)$. I didn’t spell out this claim, however the naive algorithm is $O(n^2)$. But if we skip triangle wave frequencies that are zero then we only need to do $n(\frac{1}{2} + \frac{1}{4} + \frac{1}{6} + \frac{1}{8} + ... + \frac{1}{n})$ operations. Apparently, that series grows logarithmically.

What about non-band-limited triangle waves? Well, it turns out the band-limited version is close enough you can just stick it in a non-linear least-squares solver and it’ll find you something near machine precision, despite the discontinuous Jacobian. But it’s just too slow for large problems to be all that interesting. Another thought is that if the problem is just that aliasing causes us to lose orthogonality, then can we not just upsample until the first $N$ band-limited triangle waves are effectively identical to non-band-limited? But when I tried this it would produce better results up to around 64x upsampling, and then stop, not even close to the least-squares method. I don’t really understand this at all! It could just be the problem is ill-defined but it seems unlikely to me.

At the top I said this would work for any periodic function: the DFT of any signal can be used in place of the fourier series of the triangle wave. But I’m not so interested in trying out other exotic functions like square waves as they would all have the problems laid out here, just because of how the series of functions was constructed. By band-limiting each basis function, we get a nice understanding of how the signal spans the fourier basis once shifted and sampled. But by that same token, only the complex exponential results in a series of orthogonal functions when constructed this way.

Now I can stop thinking about this.